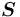 . Данная семантическая сеть представляет собой структуру (метаинформацию для) множества
. Данная семантическая сеть представляет собой структуру (метаинформацию для) множества 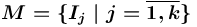 объектных информационных ресурсов, каждый из которых (
объектных информационных ресурсов, каждый из которых (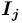 ) представлен, также, в форме семантической сети;
) представлен, также, в форме семантической сети;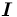 ;
;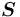 и
и 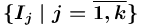 .
.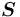 . Данная семантическая сеть представляет собой структуру (метаинформацию для) множества
. Данная семантическая сеть представляет собой структуру (метаинформацию для) множества 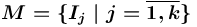 объектных информационных ресурсов, каждый из которых (
объектных информационных ресурсов, каждый из которых (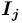 ) представлен, также, в форме семантической сети;
) представлен, также, в форме семантической сети;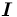 ;
;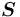 и
и 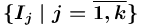 .
.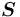 есть иерархический однородный бинарный ориентированный граф (орграф) с возможными петлями и циклами, обладающий следующими свойствами:
есть иерархический однородный бинарный ориентированный граф (орграф) с возможными петлями и циклами, обладающий следующими свойствами:
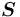 делятся на два класса:
делятся на два класса:
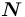 состоит из двух подмножеств:
состоит из двух подмножеств:
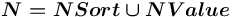 , где
, где
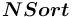 — множество всевозможных нетерминалов, описывающих сорта,
— множество всевозможных нетерминалов, описывающих сорта,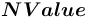 — множество всевозможных нетерминалов, описывающих значения.
— множество всевозможных нетерминалов, описывающих значения.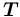 состоит из двух подмножеств:
состоит из двух подмножеств:
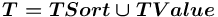 , где
, где
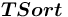 — множество всевозможных терминалов, описывающих сорта,
— множество всевозможных терминалов, описывающих сорта,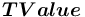 — множество всевозможных терминалов, описывающих значения.
— множество всевозможных терминалов, описывающих значения.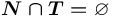 ,
, 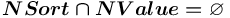 ,
, 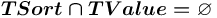 .
.
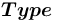 .
.
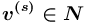 определен тип набора исходящих дуг[1], значение которого принадлежит множеству
определен тип набора исходящих дуг[1], значение которого принадлежит множеству 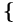 "список"[2], "альтернатива"[3]
"список"[2], "альтернатива"[3] 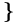 . При этом:
. При этом:
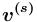 ещё не описано, то значение тип набора исходящих дуг не определён (исходящие дуги отсутствуют);
ещё не описано, то значение тип набора исходящих дуг не определён (исходящие дуги отсутствуют);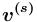 выходит только одна дуга, то считается, что тип набора исходящих дуг = "список".
выходит только одна дуга, то считается, что тип набора исходящих дуг = "список".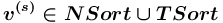 всегда определен атрибут имя, значением которого является непустая строка символов конечной длины.
всегда определен атрибут имя, значением которого является непустая строка символов конечной длины.
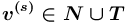 всегда определен атрибут значение.
всегда определен атрибут значение.
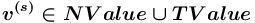 значение атрибута значение должно принадлежать одному из базовых или структурных сортов.
значение атрибута значение должно принадлежать одному из базовых или структурных сортов.
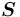 —
— 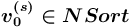 , где сортом является базовый сорт Строковое.
, где сортом является базовый сорт Строковое.
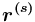 сети
сети 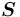 описывает направленное отношение между парой понятий: она имеет начало, конец, а также логический признак ссылка —
описывает направленное отношение между парой понятий: она имеет начало, конец, а также логический признак ссылка — 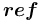 .
. 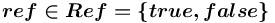 .
.
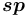 .
.
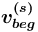 ), а то, в которое дуга входит — понятием-концом отношения (
), а то, в которое дуга входит — понятием-концом отношения (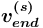 ). При этом
). При этом 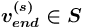 или
или 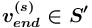 (
(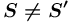 ), где
), где 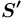 — семантическая сеть понятий, представляющая собой структуру множества
— семантическая сеть понятий, представляющая собой структуру множества 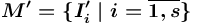 (
(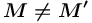 ) объектных информационных ресурсов.
) объектных информационных ресурсов.
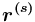 имеет признак ссылка (
имеет признак ссылка (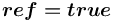 ), то понятием-концом порождаемого по
), то понятием-концом порождаемого по 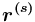 отношения-экземпляра —
отношения-экземпляра — 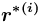 в сети
в сети 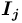 должно быть уже существующее в сети
должно быть уже существующее в сети 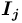 или сети
или сети 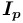 (
(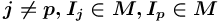 ) или сети
) или сети 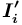 (
(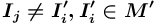 ) понятие (а не новое — порождаемое вместе с отношением
) понятие (а не новое — порождаемое вместе с отношением 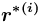 ).
).
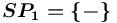 ,
, 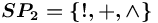 ,
, ![{{SP_{3}=\{[]\}}}](images/math/1/a/4/1a43e534d7fae7ce01e6bb560c9823a5.png) ,
, 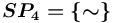 .
.
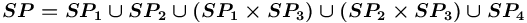 , что соответствует множеству
, что соответствует множеству
![{{\{-,!,+,\land ,(-,[]),(!,[]),(+,[]),(\land ,[]),\sim \}}}](images/math/2/9/3/293e30fe80c1f028f4560a2843302f10.png) .
.
![{{(sp,[])}}](images/math/a/d/4/ad42ccc9cf80518f13fcdc446dd4f70d.png) , где
, где 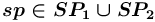 , будем записывать так:
, будем записывать так: ![{{[sp]}}](images/math/5/2/c/52ce28b30e053ec23a83fa060fa4906d.png) .
.
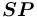 соответствует множеству
соответствует множеству ![{{\{-,!,+,\land ,[-],[!],[+],[\land ],\sim \}}}](images/math/f/a/9/fa947250f978fd0c5d4a6c9296b37b2a.png) .
.
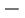 — копия ("~copy");
— копия ("~copy");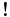 — в точности один ("~one");
— в точности один ("~one");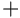 — непустое множество ("~set");
— непустое множество ("~set");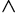 — непустая последовательность ("~seq"), элементы которой формируются автоматически и представляют собой натуральные числа;
— непустая последовательность ("~seq"), элементы которой формируются автоматически и представляют собой натуральные числа;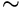 — прокси ("~proxy");
— прокси ("~proxy");![{{[]}}](images/math/b/3/f/b3ff1091f3e19865f1c9e22fa2548a63.png) — спецификатор факультативности; самостоятельно не используется, предназначен для представления следующих комбинированных спецификаторов:
— спецификатор факультативности; самостоятельно не используется, предназначен для представления следующих комбинированных спецификаторов:
![{{[-]}}](images/math/3/5/a/35ac97fce07d82c14418f4daa7447c34.png) — возможное отсутствие ("~copymm");
— возможное отсутствие ("~copymm");![{{[!]}}](images/math/4/4/3/443773b824671cf3ec3b6c2910c19a87.png) — ноль или один ("~onemm");
— ноль или один ("~onemm");![{{[+]}}](images/math/c/4/c/c4c943b99b3c53db26331891fb6c5faa.png) — возможно пустое множество ("~setmm");
— возможно пустое множество ("~setmm");![{{[\land ]}}](images/math/6/f/5/6f53ffd6aeb7ee7cc82a77384cc4d7c0.png) — возможно пустая последовательность ("~seqmm").
— возможно пустая последовательность ("~seqmm").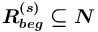 .
.
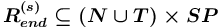 .
.
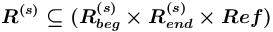 .
.
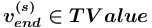 , определяется так:
, определяется так:
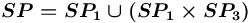 , что соответствует множеству
, что соответствует множеству ![{{\{-,[-]\}}}](images/math/9/e/b/9ebb2160c7873d44a8c6c57e9386f589.png) (иные спецификаторы не имеют смысла для данного типа вершин).
(иные спецификаторы не имеют смысла для данного типа вершин).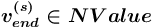 , определяется так:
, определяется так:
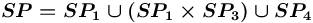 , что соответствует множеству
, что соответствует множеству ![{{\{-,[-],\sim \}}}](images/math/e/4/4/e44f5dd8a5ef7a09397a0f25688a7561.png) (иные спецификаторы не имеют смысла для данного типа вершин).
(иные спецификаторы не имеют смысла для данного типа вершин).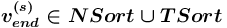 , определяется следующим образом:
, определяется следующим образом:
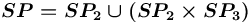 , что соответствует множеству
, что соответствует множеству ![{{\{!,+,\land ,[!],[+],[\land ]\}}}](images/math/e/c/3/ec355158b7665fb829e6af63e9cbbbb6.png) (иные спецификаторы не имеют смысла для данного типа вершин); при этом:
(иные спецификаторы не имеют смысла для данного типа вершин); при этом:
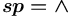 или
или ![{{sp=[\land ]}}](images/math/3/0/2/302bfa602a5056f0e2928c337a0e9941.png) допустим тогда и только тогда, когда значение атрибута значение вершины
допустим тогда и только тогда, когда значение атрибута значение вершины 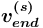 есть имя базового сорта Целое (иные сорта не имеют смысла для данных спецификаторов).
есть имя базового сорта Целое (иные сорта не имеют смысла для данных спецификаторов).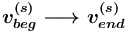 , где началом является вершина
, где началом является вершина 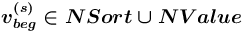 , для которой тип набора исходящих дуг = "альтернатива", а концом — вершина
, для которой тип набора исходящих дуг = "альтернатива", а концом — вершина 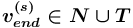 , определяется следующим образом:
, определяется следующим образом:
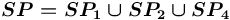 , что соответствует множеству
, что соответствует множеству 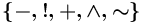 (иные спецификаторы не имеют смысла в данном контексте); при этом:
(иные спецификаторы не имеют смысла в данном контексте); при этом:
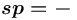 допустим тогда и только тогда, когда
допустим тогда и только тогда, когда 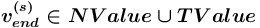 , а спецификатор
, а спецификатор 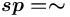 допустим тогда и только тогда, когда
допустим тогда и только тогда, когда 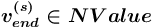 (иные спецификаторы не имеют смысла для данного типа вершин в данном контексте);
(иные спецификаторы не имеют смысла для данного типа вершин в данном контексте);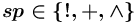 допустим тогда и только тогда, когда
допустим тогда и только тогда, когда 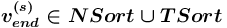 (иные спецификаторы не имеют смысла для данного типа вершин в данном контексте).
(иные спецификаторы не имеют смысла для данного типа вершин в данном контексте). (
(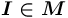 ) совпадает с определением семантической сети
) совпадает с определением семантической сети 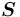 за исключением п. 4, который для сети
за исключением п. 4, который для сети  формулируется следующим образом:
формулируется следующим образом:
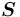 .
. делятся на два класса:
делятся на два класса:
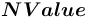 .
.
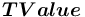 (
(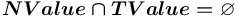 ).
).
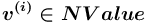 определен тип набора исходящих дуг, значение которого есть "список" (если содержание вершины
определен тип набора исходящих дуг, значение которого есть "список" (если содержание вершины 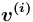 ещё не описано, то значение тип набора исходящих дуг не определён (исходящие дуги отсутствуют)).
ещё не описано, то значение тип набора исходящих дуг не определён (исходящие дуги отсутствуют)).
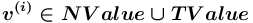 всегда определен атрибут значение, значение которого должно принадлежать одному из базовых или структурных сортов.
всегда определен атрибут значение, значение которого должно принадлежать одному из базовых или структурных сортов.
 —
— 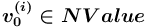 , значение атрибута значение которого принадлежит базовому сорту Строковое.
, значение атрибута значение которого принадлежит базовому сорту Строковое.
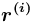 сети
сети  описывает направленное отношение между парой понятий: она имеет начало и конец. Начало и конец отношения характеризуются связанным с ними понятием.
описывает направленное отношение между парой понятий: она имеет начало и конец. Начало и конец отношения характеризуются связанным с ними понятием.
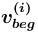 ), а то, в которое дуга входит — понятием-концом отношения (
), а то, в которое дуга входит — понятием-концом отношения (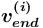 ).
).
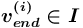 или
или 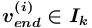 (
(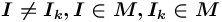 ) или
) или 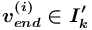 (
(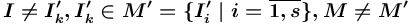 )
)
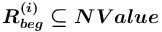 .
.
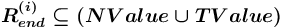 .
.
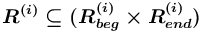 .
.
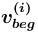 — текущее понятие из сети понятий
— текущее понятие из сети понятий  , представляющей информацию (объектный информационный ресурс);
, представляющей информацию (объектный информационный ресурс);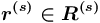 — отношение-прототип — отношение из сети понятий
— отношение-прототип — отношение из сети понятий 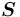 , представляющей метаинформацию, на основе которого порождаются отношения в сети понятий
, представляющей метаинформацию, на основе которого порождаются отношения в сети понятий  ;
;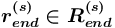 — конец отношения
— конец отношения 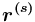 ;
;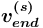 — понятие-конец отношения
— понятие-конец отношения 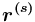 ;
;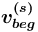 — понятие-начало отношения
— понятие-начало отношения 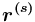 ;
;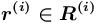 — порождаемое отношение-экземпляр в сети понятий
— порождаемое отношение-экземпляр в сети понятий  ;
;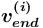 — понятие-конец отношения
— понятие-конец отношения 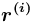 .
.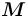 определяется структурой
определяется структурой 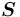 с помощью процесса порождения, в котором по структуре
с помощью процесса порождения, в котором по структуре 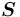 порождается информационный ресурс
порождается информационный ресурс  , принадлежащий множеству
, принадлежащий множеству 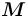 .
.
 она представлена единственной вершиной — понятием-источником
она представлена единственной вершиной — понятием-источником 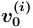 с произвольным значением атрибута значение (
с произвольным значением атрибута значение (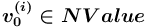 ), которая поставлена в соответствие понятию-источнику сети
), которая поставлена в соответствие понятию-источнику сети 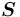 —
— 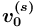 .
.
 (
(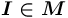 ) на основе сети
) на основе сети 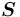 состоит в порождении в
состоит в порождении в  множества отношений-экземпляров вида
множества отношений-экземпляров вида 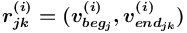 , где
, где 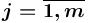 ,
, 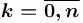 ;
; 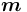 ,
, 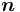 — натуральные числа, на основе множества отношений-прототипов
— натуральные числа, на основе множества отношений-прототипов 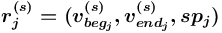 из
из 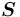 .
.
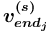 нетерминальным или терминальным понятием, от спецификатора множественности
нетерминальным или терминальным понятием, от спецификатора множественности 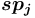 и от значения типа набора исходящих дуг для
и от значения типа набора исходящих дуг для 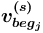 — в зависимости от них порождается один или множество нетерминалов, либо один или множество терминалов в
— в зависимости от них порождается один или множество нетерминалов, либо один или множество терминалов в  .
.
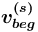 есть "список", и из неё выходят дуги
есть "список", и из неё выходят дуги 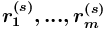 , не имеющие спецификатора факультативности ("
, не имеющие спецификатора факультативности ("![{{[]}}](images/math/b/3/f/b3ff1091f3e19865f1c9e22fa2548a63.png) "), а также дуги
"), а также дуги 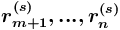 , имеющие спецификатор факультативности ("
, имеющие спецификатор факультативности ("![{{[]}}](images/math/b/3/f/b3ff1091f3e19865f1c9e22fa2548a63.png) "), то множеством отношений-прототипов, на основе которых порождаются отношения в сети понятий
"), то множеством отношений-прототипов, на основе которых порождаются отношения в сети понятий  , является непустое множество, элементами которого являются дуги
, является непустое множество, элементами которого являются дуги 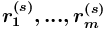 , а также, возможно, некоторые из дуг
, а также, возможно, некоторые из дуг 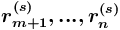 .
.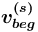 есть "список", и из неё выходят дуги
есть "список", и из неё выходят дуги 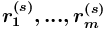 (
(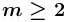 ), имеющие спецификатор факультативности ("
), имеющие спецификатор факультативности ("![{{[]}}](images/math/b/3/f/b3ff1091f3e19865f1c9e22fa2548a63.png) "), то в сети понятий
"), то в сети понятий  из вершины
из вершины 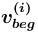 должна выходить хотя бы одна дуга.
должна выходить хотя бы одна дуга.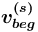 есть "альтернатива", и из неё выходят дуги
есть "альтернатива", и из неё выходят дуги 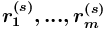 , то в сети понятий
, то в сети понятий  из вершины
из вершины 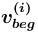 порождение возможно только по одной из дуг
порождение возможно только по одной из дуг 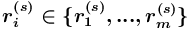 (
(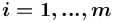 ).
).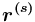 не имеет признака ссылка (
не имеет признака ссылка (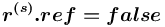 ), то:
), то:
 создаётся новая вершина
создаётся новая вершина 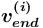 , соответствующая вершине
, соответствующая вершине 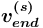 , а также отношение к ней вида
, а также отношение к ней вида 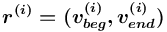 , либо
, либо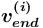 — уже существующая в сети
— уже существующая в сети  или
или 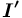 (
(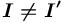 ) вершина, соответствующая вершине
) вершина, соответствующая вершине 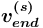 , и в сети понятий
, и в сети понятий  создаётся только отношение к
создаётся только отношение к 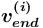 вида
вида 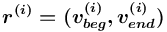 .
.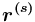 имеет признак ссылка (
имеет признак ссылка (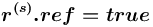 [5]
[5] 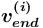 — уже существующая в сети
— уже существующая в сети  или
или 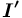 (
(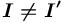 ) вершина, соответствующая вершине
) вершина, соответствующая вершине 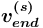 , и в сети понятий
, и в сети понятий  создаётся только отношение к
создаётся только отношение к 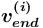 .
.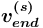 — понятие-источник сети, представляющей описание структуры Языка ИРУО, то ей соответствует любая вершина
— понятие-источник сети, представляющей описание структуры Языка ИРУО, то ей соответствует любая вершина 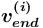 :
: 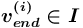 или
или 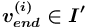 (
(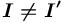 ). Таким образом, по такому
). Таким образом, по такому 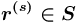 в сети понятий
в сети понятий  можно сделать:
можно сделать:
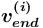 от понятия
от понятия 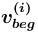 ) — если
) — если 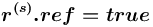 ;
;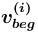 в сети понятий
в сети понятий  , и, таким образом, не соответствующий какому-либо фрагменту в сети понятий
, и, таким образом, не соответствующий какому-либо фрагменту в сети понятий 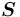 или
или 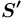 (
(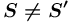 ) — если
) — если 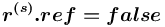 .
. по заданному отношению-прототипу
по заданному отношению-прототипу 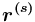 . Каждое правило охватывает сразу два случая: нефакультативный спецификатор у
. Каждое правило охватывает сразу два случая: нефакультативный спецификатор у 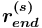 и его факультативный вариант (
и его факультативный вариант (![{{[sp]}}](images/math/5/2/c/52ce28b30e053ec23a83fa060fa4906d.png) ). В данном контексте эти случаи неразличимы, поскольку считается, что
). В данном контексте эти случаи неразличимы, поскольку считается, что 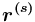 является элементом множества отношений-прототипов, на основе которых порождаются отношения в сети понятий
является элементом множества отношений-прототипов, на основе которых порождаются отношения в сети понятий  , сформированного согласно п. 1 раздела Общие правила порождения содержания понятий.
, сформированного согласно п. 1 раздела Общие правила порождения содержания понятий.
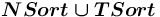 ), могут помечаться одним из следующих спецификаторов множественности:
), могут помечаться одним из следующих спецификаторов множественности: ![{{\{!,+,\land ,[!],[+],[\land ]\}}}](images/math/e/c/3/ec355158b7665fb829e6af63e9cbbbb6.png) . В зависимости от него в сети
. В зависимости от него в сети  может быть порождено единственное, либо множество понятий, описывающих значения (
может быть порождено единственное, либо множество понятий, описывающих значения (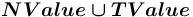 ), принадлежащие заданному сорту.
), принадлежащие заданному сорту.
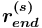 имеет вид
имеет вид 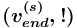 или
или ![{{(v_{{end}}^{{(s)}},[!])}}](images/math/d/c/a/dca63f717520ca841cc8be4d7ce7f200.png) , где
, где 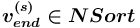 (
(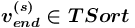 ), т.е.
), т.е. 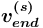 представляет собой пару [<имя>, <сорт>], где <сорт> является одним из базовых или структурных сортов, то порождается отношение
представляет собой пару [<имя>, <сорт>], где <сорт> является одним из базовых или структурных сортов, то порождается отношение 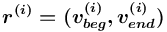 , где:
, где:
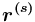 есть ложь, то
есть ложь, то
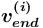 = новое нетерминальное (терминальное) понятие в сети
= новое нетерминальное (терминальное) понятие в сети  , описывающее значение (
, описывающее значение (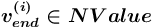 (
(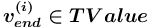 )), которому задается значение (значение атрибута значение), принадлежащее сорту <сорт>, либо
)), которому задается значение (значение атрибута значение), принадлежащее сорту <сорт>, либо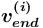 = уже существующее в сети
= уже существующее в сети  или
или 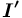 (
(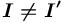 ) понятие, соответствующее понятию
) понятие, соответствующее понятию 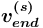 ;
;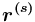 есть истина, то
есть истина, то 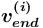 = уже существующее в сети
= уже существующее в сети  или
или 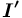 (
(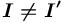 ) понятие, соответствующее понятию
) понятие, соответствующее понятию 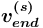 .
.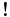 (в точности один) или
(в точности один) или ![{{[!]}}](images/math/4/4/3/443773b824671cf3ec3b6c2910c19a87.png) (ноль или один), то в
(ноль или один), то в  создаётся единственное нетерминальное (терминальное) понятие
создаётся единственное нетерминальное (терминальное) понятие 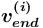 с заданным значением сорта <сорт> и отношение от понятия
с заданным значением сорта <сорт> и отношение от понятия 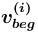 к нему, либо отношение от понятия
к нему, либо отношение от понятия 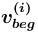 к уже существующему в
к уже существующему в  или
или 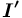 (
(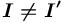 ) понятию, соответствующему понятию-концу отношения-прототипа.
) понятию, соответствующему понятию-концу отношения-прототипа.
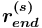 имеет вид
имеет вид 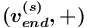 или
или ![{{(v_{{end}}^{{(s)}},[+])}}](images/math/6/2/5/62565772233b6822fe7998e969b7e20a.png) , где
, где 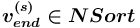 (
(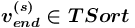 ), т.е.
), т.е. 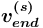 представляет собой пару [<имя>, <сорт>], где <сорт> является одним из базовых или структурных сортов, то
представляет собой пару [<имя>, <сорт>], где <сорт> является одним из базовых или структурных сортов, то 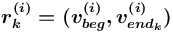 , где
, где 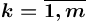 (
(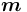 — натуральное число) и:
— натуральное число) и:
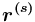 есть ложь, то
есть ложь, то
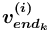 = новое нетерминальное (терминальное) понятие в сети понятий
= новое нетерминальное (терминальное) понятие в сети понятий  , описывающее значение (
, описывающее значение (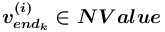 (
(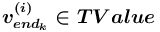 )), которому задается значение (значение атрибута значение), принадлежащее сорту <сорт>, либо
)), которому задается значение (значение атрибута значение), принадлежащее сорту <сорт>, либо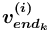 = уже существующее в сети
= уже существующее в сети  или
или 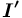 (
(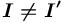 ) понятие, соответствующее понятию
) понятие, соответствующее понятию 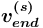 ;
;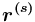 есть истина, то
есть истина, то 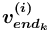 = уже существующее в сети
= уже существующее в сети  или
или 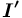 (
(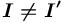 ) понятие, соответствующее понятию
) понятие, соответствующее понятию 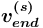 .
.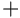 (непустое множество) или
(непустое множество) или ![{{[+]}}](images/math/c/4/c/c4c943b99b3c53db26331891fb6c5faa.png) (возможно пустое множество), то в
(возможно пустое множество), то в  создаётся непустое множество отношений
создаётся непустое множество отношений 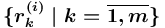 , у каждого из которых нетерминальное (терминальное) понятие
, у каждого из которых нетерминальное (терминальное) понятие 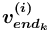 с заданным значением сорта <сорт> соответствует понятию-концу отношения-прототипа и является либо новым (созданным вместе с отношением), либо уже существующим в
с заданным значением сорта <сорт> соответствует понятию-концу отношения-прототипа и является либо новым (созданным вместе с отношением), либо уже существующим в  или
или 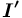 (
(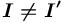 ) понятием. Таким образом создаваемые понятия образуют подцепь значений сорта <сорт>.
) понятием. Таким образом создаваемые понятия образуют подцепь значений сорта <сорт>.
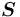 имеет вид:
имеет вид:
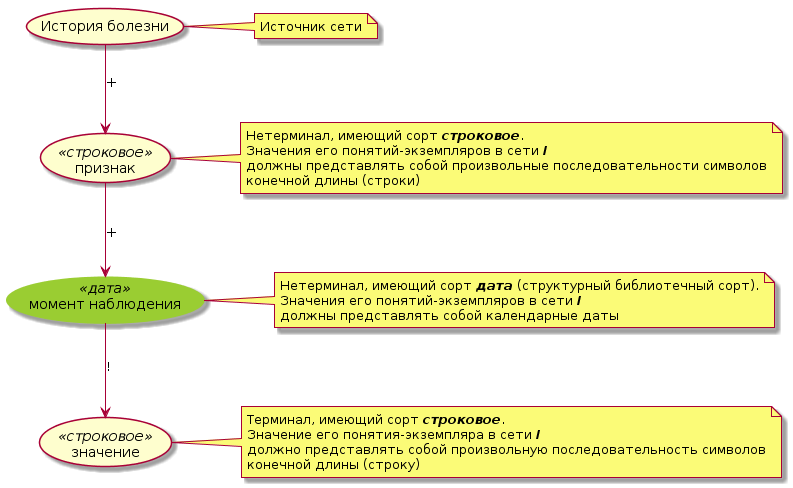
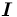 может иметь следующий вид:
может иметь следующий вид:
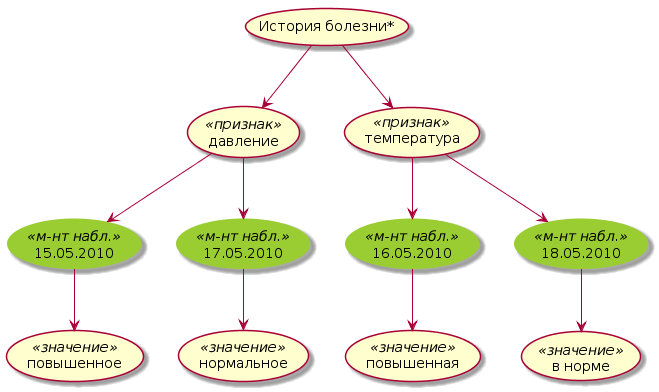
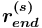 имеет вид
имеет вид 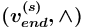 или
или ![{{(v_{{end}}^{{(s)}},[\land ])}}](images/math/4/2/4/4240b4afb68104c5fb659d100533d711.png) , где
, где 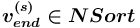 (
(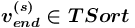 ), т.е.
), т.е. 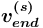 представляет собой пару [<имя>, <сорт>], где <сорт> является базовым сортом Целое (<сорт> = Целое), то
представляет собой пару [<имя>, <сорт>], где <сорт> является базовым сортом Целое (<сорт> = Целое), то 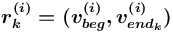 , где
, где 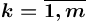 (
(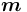 — натуральное число) и
— натуральное число) и 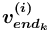 = новое нетерминальное (терминальное) понятие в сети понятий
= новое нетерминальное (терминальное) понятие в сети понятий  , описывающее значение (
, описывающее значение (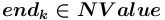 (
(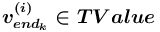 )), значение которого (значение атрибута значение, принадлежащее сорту Целое) есть натуральное число
)), значение которого (значение атрибута значение, принадлежащее сорту Целое) есть натуральное число 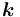 =
= 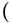 количество порождённых по
количество порождённых по 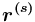 потомков понятия
потомков понятия 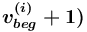 ;
;
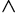 (непустая последовательность) или
(непустая последовательность) или ![{{[\land ]}}](images/math/6/f/5/6f53ffd6aeb7ee7cc82a77384cc4d7c0.png) (возможно пустая последовательность), то в
(возможно пустая последовательность), то в  создаётся непустая последовательность понятий
создаётся непустая последовательность понятий 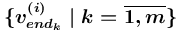 (значение понятия
(значение понятия 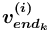 есть
есть 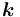 ), соответствующих понятию-концу отношения-прототипа, и отношения к ним от понятия
), соответствующих понятию-концу отношения-прототипа, и отношения к ним от понятия 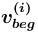 . Таким образом создаваемые понятия образуют монотонно возрастающую последовательность натуральных чисел.
. Таким образом создаваемые понятия образуют монотонно возрастающую последовательность натуральных чисел.
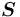 имеет вид:
имеет вид:
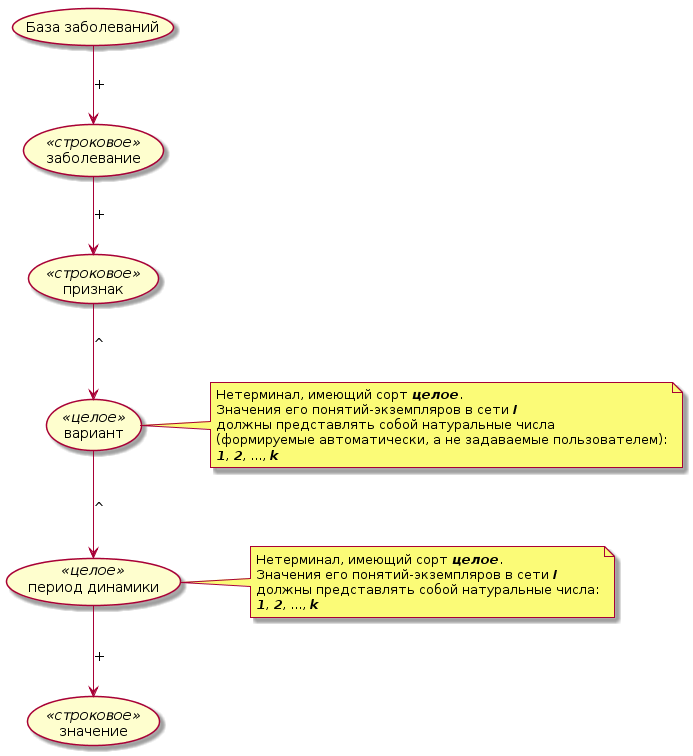
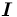 может иметь следующий вид:
может иметь следующий вид:
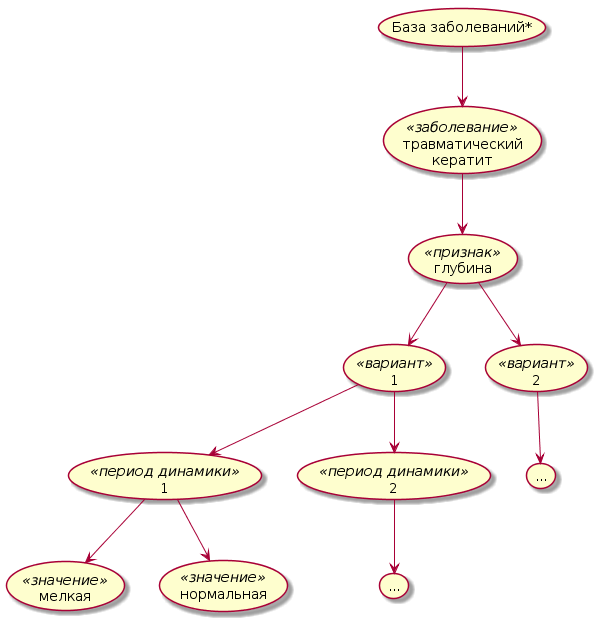
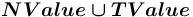 ) могут представлять только константные значения, принадлежащие одному из базовых или структурных сортов. Концы дуг, входящих в такие понятия, всегда помечаются одним из следующих спецификатором множественности:
) могут представлять только константные значения, принадлежащие одному из базовых или структурных сортов. Концы дуг, входящих в такие понятия, всегда помечаются одним из следующих спецификатором множественности: ![{{\{-,[-],\sim \}}}](images/math/e/4/4/e44f5dd8a5ef7a09397a0f25688a7561.png) — для
— для 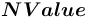 и
и ![{{\{-,[-]\}}}](images/math/9/e/b/9ebb2160c7873d44a8c6c57e9386f589.png) — для
— для 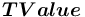 .
.
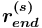 имеет вид
имеет вид 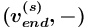 или
или ![{{(v_{{end}}^{{(s)}},[-])}}](images/math/2/a/c/2ac76502d08a4fe0444dec822aca3813.png) , где
, где 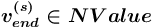 (
(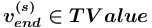 ), то
), то 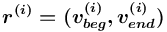 , где:
, где:
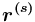 есть ложь, то
есть ложь, то 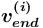 = новое нетерминальное (терминальное) понятие в сети
= новое нетерминальное (терминальное) понятие в сети  , описывающее значение (
, описывающее значение (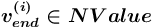 (
(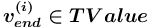 )), являющееся копией понятия
)), являющееся копией понятия 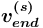 (т.е. значение атрибута значение понятия
(т.е. значение атрибута значение понятия 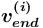 совпадает со значением атрибута значение понятия
совпадает со значением атрибута значение понятия 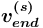 );
);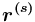 есть истина, то
есть истина, то 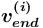 = уже существующее в сети
= уже существующее в сети  или
или 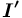 (
(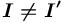 ) понятие, соответствующее понятию
) понятие, соответствующее понятию 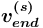 .
.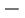 (копия) или
(копия) или ![{{[-]}}](images/math/3/5/a/35ac97fce07d82c14418f4daa7447c34.png) (возможное отсутствие), то в
(возможное отсутствие), то в  создаётся понятие, являющееся копией понятия-конца отношения-прототипа, и отношение от понятия
создаётся понятие, являющееся копией понятия-конца отношения-прототипа, и отношение от понятия 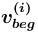 к нему, либо отношение от понятия
к нему, либо отношение от понятия 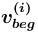 к уже существующему в
к уже существующему в  или
или 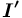 (
(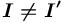 ) понятию, соответствующему понятию-концу отношения-прототипа.
) понятию, соответствующему понятию-концу отношения-прототипа.
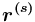 его
его 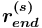 имеет вид
имеет вид 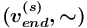 , где
, где 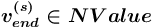 , то оно не может быть использовано для порождения отношений в
, то оно не может быть использовано для порождения отношений в  . В этом случае в качестве отношений-прототипов для порождения новых отношений и понятий в
. В этом случае в качестве отношений-прототипов для порождения новых отношений и понятий в  должны рассматриваться отношения, исходящие из
должны рассматриваться отношения, исходящие из 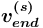 , и т.д.
, и т.д.
Проблемно-независимая предметная область / Языки / Язык ИРУО { Конструктивные элементы Языка ИРУО ~ALT { ~alt ОПИСАТЬ ВАРИАНТ АЛЬТЕРНАТИВЫ { ~list ОПИСАТЬ ЭЛЕМЕНТ СПИСКА { ~list -> ОПИСАТЬ ЭЛЕМЕНТ СПИСКА; ~alt -> ОПИСАТЬ ВАРИАНТ АЛЬТЕРНАТИВЫ; } ~alt -> ОПИСАТЬ ВАРИАНТ АЛЬТЕРНАТИВЫ; } ~list -> ОПИСАТЬ ЭЛЕМЕНТ СПИСКА; } ~alt -> ОПИСАТЬ ВАРИАНТ АЛЬТЕРНАТИВЫ; ~list -> ОПИСАТЬ ЭЛЕМЕНТ СПИСКА; }
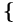 "истина", "ложь"
"истина", "ложь"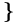 .
.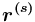 —
— ![{{sp\notin \{\land ,[\land ],\sim \}}}](images/math/9/3/e/93eedee30a30085f8905f4c804fd217e.png)